Главная » Публицистика

0 ... 18 19 20 21 22 23 24 ... 159

ние элементарного (минимального) цикла или элементарного кольца (например, кольцо а б в г яа рис. III.2).

Смешанные сети имеют .свойства как кольцевых, так и разветвленных сетей.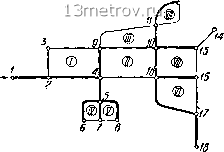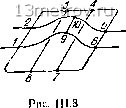

Рис. III.7

Для плоской сети любого типа может быть установлено следующее соотношение между числом ее участков р, узлов т и элементарных колец п:

р = п + т - 1,

п = р - m -f 1.

Это соотношение может быть получено как следствие теоремы Эйлера о многогранниках.

Для разветвленной сети п=0 и, следовательно,

р = т - \,

т. е. число узлов всегда на единицу меньше числа участков.

Очевидно, что для превращения кольцевой сети в разветвленную необходимо удалить п ее участков (по одному из каждого кольца). Полученная таким образом сеть называется «деревом» кольцевой сети. Из каждой кольцевой сети можно получить много вариантов дерева. Число вершин дерева всегда остается равным числу вершин соответствующей кольцевой сети.

В практике встречаются водопроводные сети, представляющие собой пространственный граф, который не может быть уложен на плоскость. Например, при пересечении в плане водопроводных линий, прокладываемых (расположенных) фактически в разных плоскостях, одни трубы проходят по виадуку (или мосту) над улицей, вдоль которой идут другие трубы. Иногда трубы каждой из этих категорий соединяют между собой перемычками (9-10 на рис. III.8).

Для пространственной сети соотношение между числом ее участков р и узлов т выражается так:

р - m + I = V,

где V - так называемое цикломатическое число; всегда vi.

Во многих пространственных сетях (содерлащих циклы) v<.n.

§ 21. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ О РАСЧЕТЕ ВОДОПРОВОДНЫХ СЕТЕЙ

Целью расчета сети является определение экономически наивыгоднейших диаметров труб всех ее участков и потерь напора в них. Однако сеть нельзя рассчитывать изолированно от всего комплекса гидравлически взаимосвязанных сооружений системы подачи и распределения воды (насосных станций, водоводов и напорных аккумулирующих емкостей).

Само понятие экономически наивыгоднейшего диаметра (см. § 18) возникло из рассмотрения условий совместной работы водопроводных линий и водопитателя (насосной станции), затрачивающего энергию на подъем воды.

а) \ Згз

о 13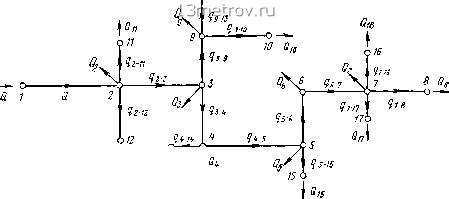

				1 -

Рис. III.9

Основы полного технико-экономического расчета сетей приводятся далее, в главе 7.

В практике проектирования, как было сказано, для приближенного определения экономически наивыгоднейших диаметров участков сети эти участки можно рассматривать как независимо работающие линии. Тогда их диаметры определяются по формуле с1=Э Q или по таблице предельных экономических расходов (приложение I).

При любых методах расчета для нахождения диаметров участков сети необходимо знать расчетные расходы в этих участках.

Для сети, которая подвергается расчету, всегда известны (заданы) ее конфигурация, длины участков и отборы воды в узлах - действительные или фиктивные (найденные в соответствии с указаниями § 17). Сети, подготовленные к расчету, показаны на рис. III.9.

При наличии одного водопитателя и отсутствии нефиксированных отборов (см. § 17) подача воды водопитателем будет также известна и равна сумме отборов Qt.

Для нахождения расходов воды Qi-k в р участках сети могут быть использованы уравнения первого закона Кирхгофа, выражающие баланс расходов в узлах - «узловые уравнения»:

2(?г-Ь 4 Qx = О, (III 2)

где i - номер узла.

При этом расходы, приходящие к узлу, условно считают положительными, а уходящие от узла (включая отбор)-отрицательными.

Число таких (независимых) уравнений для указанных условий питания сети будет т-1, где т - число узлов сети.

Для одного из узлов уравнение баланса расходов превращается в тождество (так как сумма всех отборов известна и равна подаче Q).

Так как в разветвленной сети всегда р = т - 1, то очевидно, что указанного числа узловых уравнений достаточно для определения всех неизвестных qi-n.

Таким образом, если в узлах разветвленной сети (с одним источником питания) заданы отборы воды, то расходы во всех ее участках (и по направлению, и по величине) определяются единственно возможным образом. Это является следствием того свойства разветвленной сети, что от любого ее узла до начального узла имеется только один возможный путь.

Легко видеть, что для сети на рис. П1.9, а, идя от наиболее удаленного узла 8 к начальному узлу У, можно путем последовательного сложения узловых отборов Qi получить значения расходов qi-h во всех участках сети. По этим расходам могут быть получены (приближенными или точными методами) искомые экономичные диаметры.

В кольцевых сетях значения расходов воды в участках должны удовлетворять одновременно не только уравнениям первого закона Кирхгофа [уравнениям (П1.2)], но и уравнениям второго закона Кирхгофа.

Для гидравлических сетей, как известно, эти уравнения (контурные уравнения) выражают равенство нулю алгебраической суммы потерь напора в каждом из колец сети /:

Число уравнений (П1.3) равно числу элементарных колец сети п. Вместе с т - 1 узловыми уравнениями мы будем иметь n+m-\=р уравнений для определения р неизвестных расходов в участках.

Из приведенной схемы кольцевой сети (рис. П1.9, б) легко видеть, что при заданных узловых отборах можно найти неограниченное число вариантов значений расходов qi-h, которые удовлетворяли бы уравнениям 2<7i-fe+Qi = 0 во всех узлах. Это является следствием того, что в кольцевой сети между любыми двумя ее узлами можно наметить несколько путей.

Рассматривая систему уравнений (П1.3), легко видеть, что кроме неизвестных расходов qi-h в них входят также неизвестные диаметры участков с1г-к (так как величины s~h выражаются в функции диаметров). Таким образом, отыскивая расходы qi-n, чтобы определить по ним диаметры, мы убеждаемся, что значения расходов qi-n в участках кольцевой сети в свою очередь зависят от диаметров.

Это соответствует физическому смыслу законов движения воды в кольцевых сетях. Любые изменения диаметров любых участков кольцевой сети неизбежно вызывают перераспределение расходов во всей сети, т. е. изменение расходов во всех ее участках. При любом распределении расходов будут автоматически удовлетворяться уравнения и первого и второго закона Кирхгофа.

Для одновременного нахождения неизвестных qi-h и rfi-ft, т. е. всех 2 р неизвестных, полученных систем уравнений (П1.2) и (П1.3) недостаточно.

Рассматривая пока задачу расчета сети без привлечения уравнений экономичности, т. е. не обращаясь к методам полного технико-эко-

0 ... 18 19 20 21 22 23 24 ... 159