
 | |
|
Главная » Публицистика 0 ... 96 97 98 99 100 101 102 ... 159 расширения песка. Степень расширения песка е может быть выражена через толщину слоя фильтрующего материала Lq и толщину этого слоя, «расширившегося» при промывке, L: Отсюда Поёершость песка при (ралыпробанш S \ S Промывная веда Рис. V.40 Если поверхность песка до промывки во время фильтрования занимала положение аа (рис. V.40), то при промывке песок поднимется, и поверхность взмученной массы песка, поддерживаемого восходящими токами воды, займет некоторое положение бб. Высота подъема песка будет тем больше, чем больше скорость подъема промывной воды, т. е. чем больше интенсивность промывки Кроме того, высота подъема частиц песка зависит от температуры воды. Чем ниже температура воды, а следовательно, чем больше ее вязкость, тем выше будут подниматься при той же скорости промывки частицы промываемого песка. Расширение песка происходит лишь при условии, если интенсивность промывки превышает некоторое критическое для данного случая значение. Весьма интересные теоретические исследования и эксперименты по промывке скорых фильтров были проведены в Академии коммунального хозяйства Д. М. Минцем и С. А, Шубертом. При взвешивании песка промывной водой сила тяжести песка (в воде) уравновешивается разностью сил давления у нижней и верхней поверхностей взвешенного слоя. Относя названные силы к 1 м площади фильтра, можем написать G = AP. Вес взвешенного в воде слоя песка на 1 м площади фильтра G = (pn p)g(l - mo)Lo, где рп и р - плотность соответственно песка и воды; то - пористость загрузки до расширения. Перепад сил давления АР t= Yi - р gh. Подставляя в основное уравнение динамического равновесия полученные выражения для G и АР, определим из него потери напора во взвешенном слое Рп - (I - о) Lo Из этой формулы следует, что потери напора (и перепад сил давления) в слое взвешенного песка постоянны. Они не зависят от скорости восходящего движения воды. Таким образом, с изменением интенсивности промывки (сверх критических значений) изменяются степень расширения и толщина взвешенного слоя, но потери напора во взвешенном слое остаются неизменными. Движение воды через слой песка, взвешенного в восходящем пото- ке, можно рассматривать как частный случай движения жидкости в пористой среде. Таким образом, устанавливается определенная аналогия между движением воды во взвешенном слое и движением ее через фильтрующий материал. Разница заключается в том, что при изменении скорости в первом случае меняется толщина слоя, но потери напора остаются постоянными, во втором случае толщина слоя остается той же, а потери напора изменяются. Для изучения законов движения воды через слой песка, взвешенного в восходящем потоке, Д. М. Минц и С. А. Шуберт использовали теорию подобия и в результате обработки опытных данных предложили формулы, позволяющие определять при этом виде движения коэффициенты сопротивления, скорости и интенсивности промывки. В соответствии с результатами этих исследований скорость движения промывной воды v (в смус) может быть выражена следующей формулой: 1.3 0.54 p0.23 j)1.77(j )0.54 d-диаметр зерен песка (для однородной загрузки); ц-коэффициент вязкости воды, зависящий от ее температуры. Если принять для кварцевого песка рп==2,62 и для воды р=1, а также использовать полученные из опыта значения параметра А и коэффициента формы зерен песка а, то формула примет такой вид: „>,о <-+"°- . ..0.54 /„ i 1л1,77., ,0,54 Ц (е+ 1) • (1 - то) • Для практических расчетов удобно вместо скорости v ввести в формулу «интенсивность промывки» q, т. е. количество воды, подаваемой для промывки фильтров на 1 м его площади (в л/с): «« (в + 1)."(1-т,Л«* Эта формула устанавливает зависимость между интенсивностью промывки и степенью расширения песка для различной крупности (и пористости) загрузки и различной температуры (а следовательно, и вязкости) воды. Полученная для q формула в представленном виде справедлива для однородной загрузки, т.е. песка с одинаковой крупностью зерен. Так как в практике песчаная загрузка фильтра всегда состоит из зерен различного диаметра, в приведенной формуле под d следует понимать эквивалентный диаметр песка. Таблица V.10
В табл. V.10 приведены значения требуемого расширения песка и соответствующие им интенсивности и длительности промывки для различных загрузок. Применение антрацитовой загрузки (как более легкой) позволяет значительно (на 70%) снизить интенсивность промывки при том же эффекте очистки фильтрующего материала. Большие значения интенсивности промывки соответствуют меньшим значениям ее длительности. Как видно из приведенных формул, при более высоких температурах воды, т.е. при меньшей ее вязкости, требуемая интенсивность промывки (при прочих равных условиях) возрастает. Таким образом, расход промывной воды летом больше, чем зимой. Верхняя промывка скорых фильтров. В качестве мероприятия, повышающего качество промывки фильтров и предотвращающего накопление остаточных загрязнений на фильтре, применяют так называемую верхнюю (или поверхностную) промывку фильтров, при которой промывная вода подается на фильтр сверху. Верхнюю промывку применяют как дополнение к основной промывке фильтра снизу обратным то- 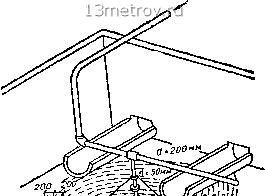 уробень Воды при начале промывки 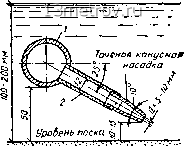 Рис. V.41 КОМ ВОДЫ И производят в сочетании с последней. Задачей верхней промывки является взмучивание загрязнений верхнего слоя фильтрующего материала. Существует два основных способа поверхностной промывки: с неподвижными промывными трубами и с вращающейся промывной трубой. При первом способе промывная вода подается на фильтр через сеть дырчатых труб, расположенных на высоте 5-7,5 см над поверхностью песка параллельно желобам для отвода промывной воды. Отверстия в трубах расположены в шахматном порядке и обращены вниз под углом 30° к горизонту. Интенсивность промывки составляет 3-4 л/{с-м). Второй способ (рис. V.41) осуществляется при помощи вращающейся трубы /, снабженной отверстиями или соплами 2, через которые вода подается на фильтр. Труба / вращается по принципу сегнерова колеса в плоскости, расположенной на 5 см выше поверхности фильтра. 0 ... 96 97 98 99 100 101 102 ... 159 |