
 | |
|
Главная » Публицистика 0 ... 28 29 30 31 32 33 34 ... 159 (предусматриваемый сортаментом труб), так же как и характеристики насосов Я=ф(Р). Из трех величин qi-k, di-k и hi~k для каждого участка сети независимыми переменными являются только две. При анализе величины W удобнее ее выражать в функции расходов и потерь напора; для этого диаметры di-h надо выразить через потери напора: /6 \ 1 п Принимая в дальнейших расчетах р = 2, получим .U7 (р, + £) S (а + <7£f ftr«/- +р{Но+Е h, ,) Q. (in. 12) напр Первая сумма распространяется па все участки сети, вторая - на участки одного из возможных путей, соединяющего насосную станцию с конечной точкой сети. Искомые величины qi-k и hi-k. должны, как было сказано, соответствовать наименьшему значению функции W. Очевидно, необходимо исследовать экстремальные значения функции W, определить их характер и попытаться найти соответствующие значения qi-k и hi-k (а следовательно, и di-k).
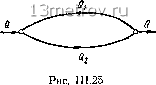 Рис. III.24 Так как расходы и потери напора в сетях связаны соответственно первым и вторым законами Кирхгофа, задача состоит в определении условного экстремума функции W при соблюдении уравнений lLqi-k-\-Q.i - = 0 для всех узлов и S/Zi ft = 0 для всех колец сети. Подобная задача может быть, как известно, решена с использованием неопределенных множителей Лагранжа путем нахождения экстремального значения некоторой функции = 1Г + U. (S<7f ;fe -f Q.) + S?., h. . В результате дифференцирования по qi-n и по hi-k, приравнивания нулю частных производных d)ldqi-k и di/dhi-k и исключения неопределенных множителей, получим две группы уравнений: п уравнений вида И т-1 уравнений вида Таким образом, формально мы получим недостающие п-\-т-1=р уравнений. Однако анализ вторых дифференциалов функции W (по qi-k и hik) показывает, что при всех практически встречающихся значениях а и m величина dW/dhf i всегда положительна, а величина dWldqf f всегда отрицательна. Следовательно, функция W является выпукло-вогнутой и не имеет экстремума. Таким образом, нахождение одновременно оптимальных значений расходов и оптимальных значений потерь напора неосуществимо. Если задаться значениями расходов воды в участках сети qt-h, то экстремальное значение функции W может быть найдено; функция W оказывается выпуклой, и величины потерь напора (а следовательно, и диаметров при заданных расходах) получаются из уравнений dW/dhi-h и соответствуют наименьшей величине W, т. е. являются наивыгоднейшими. Если же задаться значениями потерь напора, то функция W будет вогнутой, и получаемые из уравнений dWjdqi-k - 0 расходы соответствуют наибольшему значению функции W и, следовательно, являются наиневыгоднейшими. Задача определения наивыгоднейших расходов в участках кольцевой сети сводится фактически к попытке нахождения наивыгоднейшего распределения потоков воды. Но, как мы видели, экстремальное значение W - F{qi-h) соответствует не минимуму, а максимуму W. Наглядной иллюстрацией этого может служить попытка отыскания наивыгоднейшего распределения общего расхода Q по ветвям кольца с одинаковыми длинами ветвей (рис. П1.25). Анализ функции W для такого кольца показывает, что экстремальному (наибольшему) значению W соответствует распределение расхода Q поровну между двумя ветвями кольца. Наименьшее значение W будет при таком распределенип, когда весь расход Q пойдет по одной из ветвей кольца, т.е. при Qi = = Q и Q2=0. В этом случае необходимость во второй ветви отпадает и кольцо превращается в одну линию. Анализ распределения потоков по ветвям любой кольцевой сети показывает, что наивыгоднейшим будет такое распределение потоков, при котором кольцевая сеть превращается в дерево. Этим подтверждается положение, что кольцевая сеть по сравнению с разветвленной всегда будет менее экономична (для обеспечения водой заданных потребителей). Кольцевание сетей есть мера по повышению надежности сети и, естественно, вызывает дополнительные затраты. Задавать начальное потокораспределение (см. § 22) необходимо исходя из требований надежности. Если это требование удовлетворено, то соответствующее потокораспределение может быть принято как заданное для определения наивыгоднейших диаметров. § 29. МЕТОДЫ ТЕХНИКО-ЭКОНОМИЧЕСКОГО РАСЧЕТА СЕТЕЙ ПРИ ЗАДАННЫХ ЗНАЧЕНИЯХ РАСХОДОВ ВОДЫ В ЛИНИЯХ СЕТИ При заданных значениях расходов в участках сети неизвестными являются значения диаметров йг-п или потерь напора hi-n. Практически, как было сказано, удобнее искать значения hi-u, после чего однозначно определяются и соответствующие диаметры di-u. Необходимая для этого система уравнений получается в результате дифференцирования функции стоимости W по Ы-п, т. е. из системы уравнений вида dW/dhi-k=0. В развернутом виде (например, для сети, указанной на рис. И1.26) эта система имеет вид: а-\-т а+т а+т - AQ = 0, 2-3 "2-3 2-5 "2-5 = 0; 2-3 "2-3 =-0; 42-52-5" Л- а а+т 5-6 "-5-6 a, gh, J =0; а+т 4-5 Ч-5 - ass 5-Ь = 0; 1-6 Ч-6 - 5-6 "5-6 6-7 "б-7 а+т а+т - а-у о h 7-8 7-8 (III. 13) (S-8 К-8 + "7-8 7-8 ~ 8-9 8-9 В системе этих уравнений (число их равно числу узлов сети без од- а+т 2а ного) содержатся однотипные члены вида ai-.khi f , где aj AS=j X а+т "У / "г t-k Для всех узлов, кроме начального /, эти выражения удовлетворяют условию, аналогичному условию баланса расходов в узлах сети. Для начального узла сети уравнение выражает равенство величин at-k h k для участков, отходящих от узла 1, величине AQ, где Q - полный расход воды, подаваемой в сеть (здесь - при одном водопитателе - этот расход также известен); величина ip-\-E)bk" Значения всех величин, входящих в Р, приведены в § 28. Подобная система т-1 нелинейных уравнений с т-1 неизвестными hi-k может быть решена любым из существующих для этого методов. Относительно простой способ решения этой задачи предложен проф. Л. Ф. Мошниным. Если разделить все уравнения системы (П1.13) на Л и обозначить выражение ai-khi /Л через Xi-kQ (т.е. в частях полного расхода Q), то указанная система уравнений примет вид: Xi 2Q + Xj gQ=Q- Xj 2Q - 2-3Q - X = 0: Разделив, наконец, все эти уравнения на Q, получим т-1 уравнений, связывающих величины Xi-k. xj 2+ Xi g = 1; 1-2 2-3 2-5 ~ "2-3 - хо4 = 0; (III. 14) 0 ... 28 29 30 31 32 33 34 ... 159 |
|||||||||||||||||||||||