Главная » Публицистика

0 ... 25 26 27 28 29 30 31 ... 159

ляются единственно возможным образом без всякой увязки в соответствии с величиной отборов в их конечных точках.

Положение изменилось только для магистрали АБ, так как в нее «включены параллельно» два водопитателя.

Всякое параллельное включение элементов системы образует некоторое подобие замкнутого контура. В данном случае такой контур может быть представлен путем дополнения сети фиктивным узлом О и двумя фиктивными ветвями OA и ОБ. Предположим, что в точку О подается расход Q = SQt. Эта величина, очевидно, равна сумме пока неизвестных подач Qi и Qn.

Если фиктивным линиям придать соответственно значения расходов Qi и Qii и значения напоров Hi и Нц первого и второго водопитателя и составить для полученного фиктивного кольца (обходя его по часовой стрелке) уравнение второго закона Кирхгофа, получим (см. рис. HI.17)

Н, - (Е /1)л„м + (2 h) - Я„ = 0. (III.7)

Н, - Я„ = (S h) ~ (v h) , (III .8)

т. е. обычное уравнение, связывающее между собой пьезометрические отметки двух насосных станций, подающих воду в одну распределительную систему.

Связь между Hi и Qi, а также между Нц и Qn определяется напор-но-расходными характеристиками водопитателей, которые в общем виде могут быть представлены так:

Таким образом, уравнение (III.8) может быть представлено как функция расходов:

F (Qi) - Ф (Qii) = (2 i-k qLk)a-m - (2 qLk)b-m- ("I -Sa)

В подобной форме уравнение связи водопитателей было представлено в общем виде в § 23.

Увязка фиктивного кольца производится путем перераспределения расходов на участках магистрали А-Б и соответствующего изменения подач Qi и Qn.

Истинные значения всех этих расходов получаются при удовлетворении уравнения (111.8а). Разумеется, контурное уравнение (111.8а) должно решаться совместно с уравнениями l!qг-h-\-Qг = для всех узлов магистрали АБ и для фиктивного узла О. Последнее уравнение имеет вид:

Тот же путь решения может использоваться для схемы, показанной на рис. И1.18, когда сеть имеет один водопитатель (например, в точке Л) и один нефиксированный отбор (например, в точке Б). Роль нефиксированного отбора играет водонапорная башня в периоды ее питания от сети (в моменты транзита воды в башню). Для такого случая на рис. И1.18 показаны схема распределения воды в сети и фиктивное кольцо, а на рис. III.19 дано расположение пьезометрических линий.

Если соединить все точки отбора воды некоторой фиктивной линией (пунктир на рис. III.18) с точкой О, то мы получим наглядное выражение баланса расходов в узле О.

Данная схема подобна схеме действия аналоговой машины для расчета сетей (см. далее § 26).

Контурное уравнение для фиктивного кольца будет:

- Я„ =0.

в данном случае Яб = соп51 и не зависит от Qn.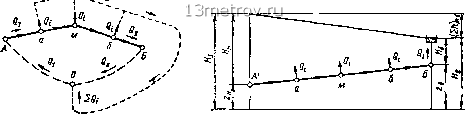

Рис. III.18

Рис. III.19

Подобное соотношение пьезометрических отметок Ян и Яб показано на рис. П1.19 для случая транзита воды в башню.

Таким образом, если в разветвленной сети суммарное число водопитателей и нефиксированных отборов е>-1, то в ее расчетную схему добавляется е-1 фиктивных колец. Что касается кольцевой сети, то в аналогичном случае (при е>-1) к реальным кольцам сети в ее расчетную схему также добавляется е-1 фиктивных колец.

Все фиктивные кольца могут быть образованы путем соединения одного фиктивного узла с узлами расположения водопитателей и нефиксированных отборов.

Соответствующая расчетная схема для кольцевой сети с двумя насосными станциями и двумя башнями представлена на рис. П1.20.

Для нахождения всех р неизвестных расходов в действительных участках сети и е неизвестных подач водопитателей, т.е. неизвест-

ных, могут быть составлены:

т узловых уравнений (для всех узлов сети)

Ъдг-к + = 0; п контурных уравнений для действительных колец

е-1 контурйых уравнений для фиктивных колец

F{Q) -ф(д) S/i. ,. т.е. всего т-\-п-\-е-\=ре уравнений. Этих уравнений достаточно для нахождения всех искомых расходов.

Найдя расходы, можно определить потери напора во всех линиях сети. Как было указано ранее, для определения пьезометрических отметок в узлах сети необходимо иметь связь пьезометрической отметки хотя бы одной точки системы с геодезической отметкой той же точки. Это требование выполняется, в частности, если в функции H=F{Q) в величину Ян введена геодезическая отметка оси насоса.

Следует отметить, что введение в систему фиктивных колец не только является средством для увеличения наглядности взаимосвязей водопитателей, но и устанавливает схему составления расчетных уравнений, необходимых для решения задачи увязки сетей при их совместной работе с водопитателями и нефиксированными отборами.

Подобные схемы широко используются для составления алгоритмов и программ расчета систем подачи и распределения воды на вычислительных машинах.

При ручных расчетах нахождение истинных расходов в системе при совместной работе сети с несколькими водопитателями производится путем последовательного приближения и является весьма трудоемким процессом.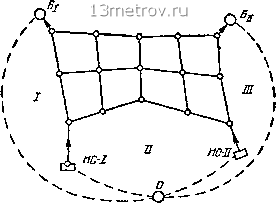

Рис. III.20

Покажем на простейшем примере возможность и путь увязки двух-кольцевой сети с водопитателем и нефиксированным отбором (рис. П1.21).

Двухкольцевая сеть питается водой от насосной станции НС по водоводу из двух параллельных линий диаметром 6 = 500 мм и длиной 500 м.

Рис. III.21

На схеме (рис. П1.21,а) в узлах сети показаны величины заданных фиксированных отборов (в л/с), около каждого участка сети показаны длины линий (в м), первоначальное распределение расходов и принятые величины диаметров.

К точке 4 примыкает водовод, соединяющий сеть с башней Б. Таким образом, мы имеем кольцевую сеть с водопитателем НС и нефиксированным отбором - башней Б для случая транзита воды в нее.

0 ... 25 26 27 28 29 30 31 ... 159